Probability Distribution Analysis
About Probability Distribution Analysis
Probability Distribution Analysis allows you to describe the Time to Failure (TTF) as a statistical distribution, which usually is characterized by a specific pattern.
Based on a query, dataset, or data that you manually enter, you can use an independent variable to generate a Probability Distribution Analysis. GE Digital APM Reliability supports four Distribution types:
About Data Censoring in a Probability Distribution Analysis
Probability Distribution Analysis supports the functionality of censoring, which accounts for the period of time from the last failure date to the analysis end date. You can censor or ignore datapoints in a Probability Distribution Analysis to estimate the probability when a failure might occur. Censoring is based on failure modes.
Censoring a datapoint means that the datapoint is excluded as a failure but included in the operating time of the Asset. If you select the Censored check box, the data in the selected row is excluded. When you create a Probability Distribution Analysis using a query or dataset as the data source, the GE Digital APM system automatically censors time values from the beginning of the Analysis Period to the first event and the time value from the last event to the end of the analysis. After the calculations for the analysis have been performed, each time that the query or dataset is refreshed, the failure data will be automatically censored.
Regardless of the data source you use, you can censor any failure data. Consider the following:
- For Maximum Likelihood Estimators (MLE), the maximum number of censored datapoints is one (1) less than the total number of datapoints.
- For Least Squares estimation, the maximum number of censored datapoints is two (2) less than the total number of datapoints.
Pump Failure
Assume that you want to determine the reasons for a pump failure.
A pump might have failed due to multiple reasons, such as rusted part, motor overheating, insufficient power supply, or power outage. Each of these reasons will have its own specific failure rate and probability density function. To determine the failure rate of "motor overheating," you must censor all other failure modes from the analysis.
Further, motor overheating might be caused due to multiple reasons, such as improper operation, improper application, and improper maintenance. The censoring feature allows you to separate the failure modes, and determine which is the dominant failure mode. Based on this information, you can decide what is needed to improve the motor performance.
Access a Probability Distribution Analysis
Procedure
About Probability Plot
The Probability Plot is a log-log plot with data overlay and confidence limits that graphically displays the probability (expressed as a percentage) of each possible value of the random variable (CDF Occurrence % vs. time). CDF Occurrence % used here is numerically equal to the value from the cumulative distribution.

The Probability Plot shows the same data as the CDF plot, just represented in a log-log format. The log-log format reflects the standard technique for representing Weibull Distribution. Log-log format Data overlay gives a visual estimate of Goodness of Fit (GOF). Data overlay also gives clues to the presence of multiple failure modes. If a single or multiple inflection points exist in the data, then there is a possibility of multiple failure modes.
Graph Features
While accessing a Probability Plot, you can:
-
Hover or tap on any datapoint to view the coordinates and the details of a datapoint.
- For an Estimated datapoint, you can view the type of distribution, the distribution parameters, and the value of R-Squared.
- For an Observed datapoint, you can view the name and the value of Variable.
-
Click or double-tap on any observed datapoint to view the data on the Distribution Data window.
- Censor a datapoint.
- Customize the appearance of the plot by using standard graph features.
- Customize the data displayed in the graph by adjusting the x-axes to vary the display range.
About PDF Plot
The Probability Density Function (PDF) plot is a lin-lin plot that counts the number of failures (or any other data) between certain time periods, creating a curve fit that estimates how many failures (failure data or any other data) you can expect to occur at a given point of time. This plot shows Density vs. Size. The term Density is used here with failure data to describe the size of the population that failed at the particular value of size (SqFt). A PDF plot helps you to answer a question such as, "What is the chance of a member of the population failing at exactly the time in question?"
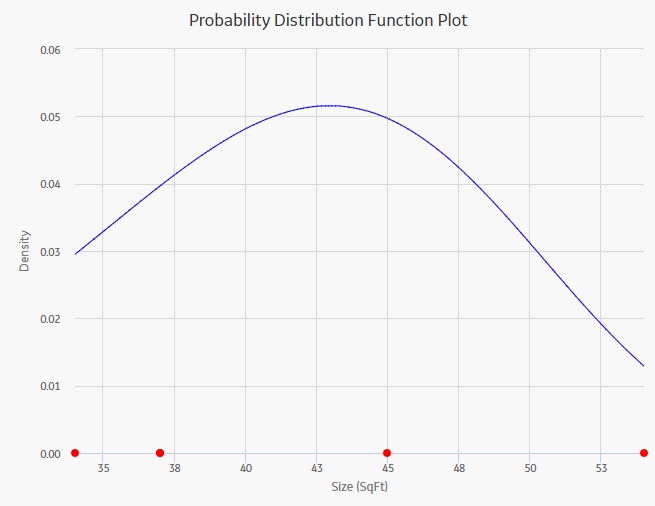
Graph Features
While accessing a PDF plot, you can:
- Hover or tap on any datapoint to view the coordinates and the details of a datapoint.
- For an Estimated datapoint, you can view the type of distribution, the distribution parameters, and the value of R-Squared.
- For an Observed datapoint, you can view the name and the value of Variable.
- Click or double-tap on any observed datapoint to view the data on the Distribution Data window.
- Censor a datapoint.
- Customize the appearance of the plot by using standard graph features.
- Customize the data displayed in the graph by adjusting the x-axes to vary the display range.
About CDF Plot
The Cumulative Distribution Function (CDF) plot is a lin-lin plot with data overlay and confidence limits. It shows the cumulative density of any data set over time (i.e., Probability vs. size). The term Probability is used in this instance to describe the size of the total population that will fail (failure data or any other data) by size (SqFt).
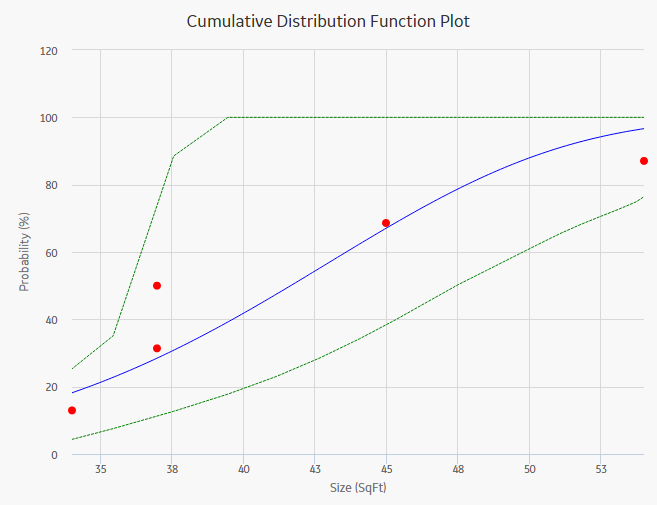
CDF plot answers a different question than PDF. For example, "What is the probability of failure at Size (SqFt)?" The CDF curve is the area under the PDF curve. The CDF accumulates all probability of failure up to the point in time in question. Since the number of failures increases with increasing size, the slope of the curve is always positive, always increasing.
Graph Features
While accessing a CDF plot, you can:
- Hover or tap on any datapoint to view the coordinates and the details of a datapoint.
- For an Estimated datapoint, you can view the type of distribution, the distribution parameters, and the value of R-Squared.
- For an Observed datapoint, you can view the name and the value of Variable.
- Click or double-tap on any observed datapoint to view the data on the Distribution Data window.
- Censor a datapoint.
- Customize the appearance of the plot by using standard graph features.
- Customize the data displayed in the graph by adjusting the x-axes to vary the display range.
Collect Data for Probability Distribution Analysis
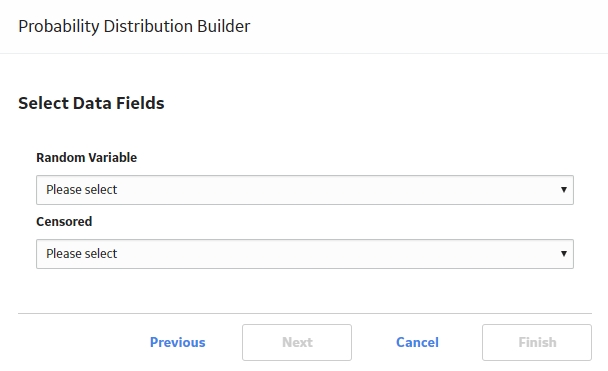
To create a Probability Distribution Analysis, you must select the field that contains the value that you want to analyze.
The following table shows the typical data needed to build and analyze Probability Distribution Analyses.
| Data Required | Data Type | Description | Behavior and Usage |
|---|---|---|---|
|
Censored | Logical |
As needed, select the field to provide censoring information. Select the field from the data source that contains a value that indicates censored values. |
This field is optional. |
|
Random Variable | Character |
If the data source is a query, the name of the random variable and the units of measure will be pre-populated based on the selection you made in the Value field on the previous screen. If you selected a different data source, type the name of the random variable in the Random Variable field and the units of measure for the random variable in the Units field. |
This field is optional.
|
|
Units | Character |
Select the units of measure for the random variable. |
This field is optional. |
|
Value | Numeric |
Select the field that contains the value you want to analyze. |
This is a required field. |
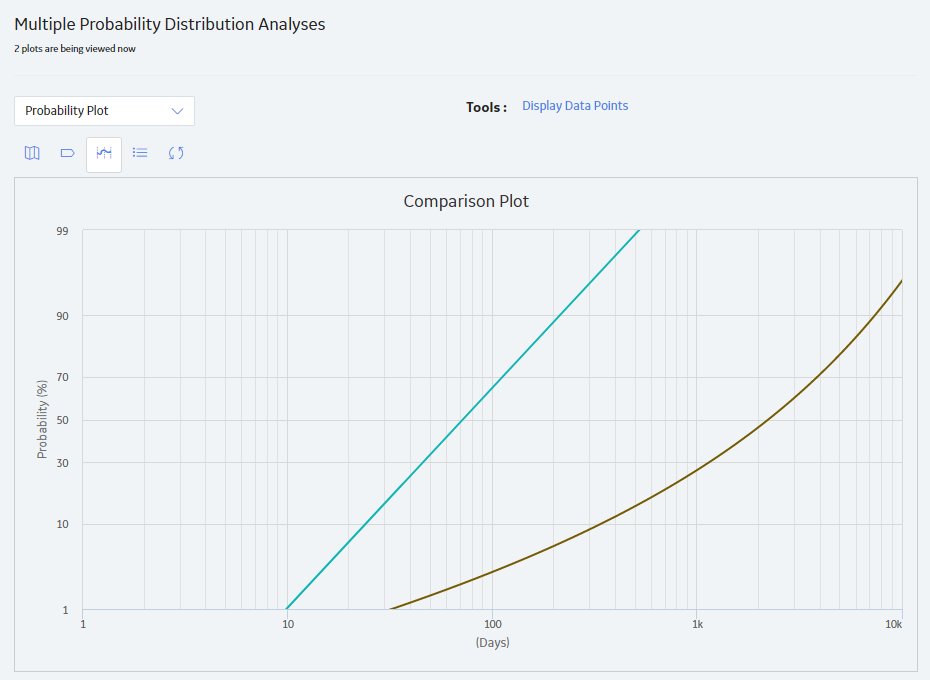
Access Multiple Probability Distribution Analyses
About this task
You can access multiple Probability Distribution Analyses and compare multiple plots for the selected analyses. You cannot modify the details of the analyses based on which the Comparison Plot is generated.
Procedure
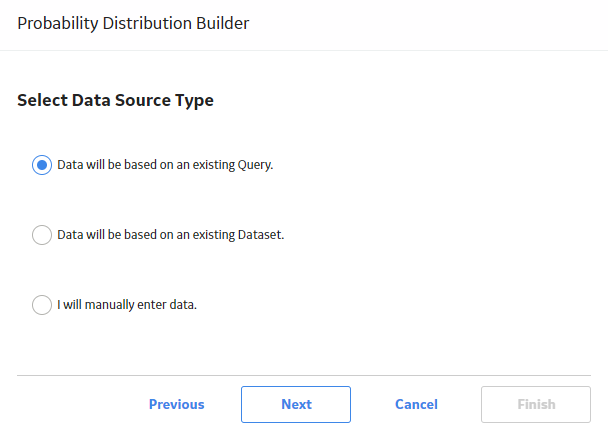
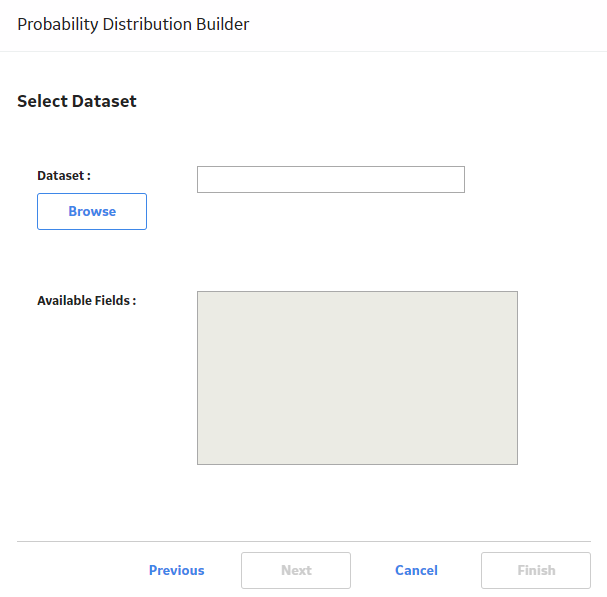
Create a Probability Distribution from an Existing Query or Dataset
Procedure
Create a Probability Distribution from Manually Entered Data
Procedure
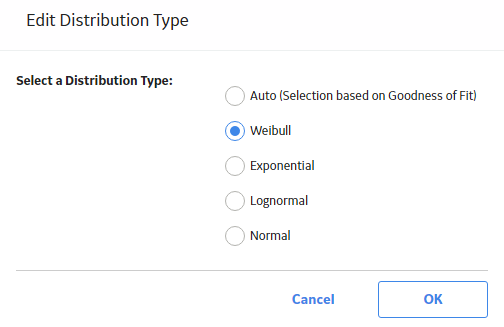
Change the Distribution Type of a Probability Distribution Analysis
About this task
When you create a Probability Distribution Analysis, the Distribution Type is set to Weibull by default. After the analysis is created, you can change the Distribution Type to one of the following:
- Normal
- Weibull
- Exponential
- Lognormal
- Triangular
- Gumbel
- Generalized Extreme Value
- Auto
You can change the Distribution Type from the Analysis Summary workspace or from any of the plot tabs in the left pane.
Procedure
About Normal Distribution
A Normal Distribution describes the spread of data values through the calculation of two parameters: mean and standard deviation. When using the Normal Distribution on time to failure data, the mean exactly equals MTBF and is a straight arithmetic average of failure data. Standard deviation (denoted by sigma) gives estimate of data spread or variance.
A Normal Distribution uses the following parameters:
- Mean: The arithmetic average of the datapoints.
- Standard Deviation: A value that represents the scatter (how tightly the datapoints are clustered around the mean).
About Weibull Distribution
A Weibull Distribution describes the type of failure mode experienced by the population (infant mortality, early wear out, random failures, rapid wear-out). Estimates are given for Beta (shape factor) and Eta (scale). MTBF (Mean Time Between Failures) is based on characteristic life curve, not straight arithmetic average.
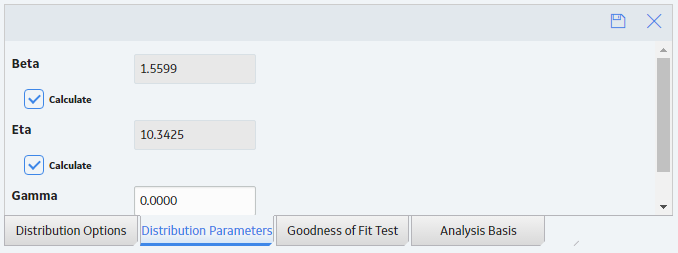
A Weibull Distribution uses the following parameters:
- Beta: Beta, also called the shape factor, controls the type of failure of the element (infant mortality, wear-out, or random).
- Eta: Eta is the scale factor, representing the time when 63.2 % of the total population is failed.
- Gamma: Gamma is the location parameter that allows offsetting the Weibull distribution on time. The Gamma parameter should be used if the datapoints on the Weibull plot do not fall on a straight line.
If the value of Beta is greater than one (1), you can perform Preventative Maintenance (PM) Optimizations. A Gamma different from a value zero (0) means that the distribution is shifted to fit the datapoints more closely.
Weibull Analysis Information
You can use the following information to compare the results of individual Weibull analyses. The following results are for good populations of equipment.
| Beta Values Weibull Shape Factor | ||||||
|---|---|---|---|---|---|---|
|
Components |
Low |
Typical |
High |
Low (days) |
Typical (days) |
High (days) |
|
Ball bearing |
0.7 |
1.3 |
3.5 |
583 |
1667 |
10417 |
|
Roller bearings |
0.7 |
1.3 |
3.5 |
375 |
2083 |
5208 |
|
Sleeve bearing |
0.7 |
1 |
3 |
417 |
2083 |
5958 |
|
Belts drive |
0.5 |
1.2 |
2.8 |
375 |
1250 |
3792 |
|
Bellows hydraulic |
0.5 |
1.3 |
3 |
583 |
2083 |
4167 |
|
Bolts |
0.5 |
3 |
10 |
5208 |
12500 |
4166667 |
|
Clutches friction |
0.5 |
1.4 |
3 |
2792 |
4167 |
20833 |
|
Clutches magnetic |
0.8 |
1 |
1.6 |
4167 |
6250 |
13875 |
|
Couplings |
0.8 |
2 |
6 |
1042 |
3125 |
13875 |
|
Couplings gear |
0.8 |
2.5 |
4 |
1042 |
3125 |
52083 |
|
Cylinders hydraulic |
1 |
2 |
3.8 |
375000 |
37500 |
8333333 |
|
Diaphragm metal |
0.5 |
3 |
6 |
2083 |
2708 |
20833 |
|
Diaphragm rubber |
0.5 |
1.1 |
1.4 |
2083 |
2500 |
12500 |
|
Gaskets hydraulics |
0.5 |
1.1 |
1.4 |
29167 |
3125 |
137500 |
|
Filter oil |
0.5 |
1.1 |
1.4 |
833 |
1042 |
5208 |
|
Gears |
0.5 |
2 |
6 |
1375 |
3125 |
20833 |
|
Impellers pumps |
0.5 |
2.5 |
6 |
5208 |
6250 |
58333 |
|
Joints mechanical |
0.5 |
1.2 |
6 |
58333 |
6250 |
416667 |
|
Knife edges fulcrum |
0.5 |
1 |
6 |
70833 |
83333 |
695833 |
|
Liner recip. comp. cyl. |
0.5 |
1.8 |
3 |
833 |
2083 |
12500 |
|
Nuts |
0.5 |
1.1 |
1.4 |
583 |
2083 |
20833 |
|
"O"-rings elastomeric |
0.5 |
1.1 |
1.4 |
208 |
833 |
1375 |
|
Packings recip. comp. rod |
0.5 |
1.1 |
1.4 |
208 |
833 |
1375 |
|
Pins |
0.5 |
1.4 |
5 |
708 |
2083 |
7083 |
|
Pivots |
0.5 |
1.4 |
5 |
12500 |
16667 |
58333 |
|
Pistons engines |
0.5 |
1.4 |
3 |
833 |
3125 |
7083 |
|
Pumps lubricators |
0.5 |
1.1 |
1.4 |
542 |
2083 |
5208 |
|
Seals mechanical |
0.8 |
1.4 |
4 |
125 |
1042 |
2083 |
|
Shafts cent. pumps |
0.8 |
1.2 |
3 |
2083 |
2083 |
12500 |
|
Springs |
0.5 |
1.1 |
3 |
583 |
1042 |
208333 |
|
Vibration mounts |
0.5 |
1.1 |
2.2 |
708 |
2083 |
8333 |
|
Wear rings cent. pumps |
0.5 |
1.1 |
4 |
417 |
2083 |
3750 |
|
Valves recip comp. |
0.5 |
1.4 |
4 |
125 |
1667 |
3333 |
|
Equipment Assemblies |
Low |
Typical |
High |
Low (days) |
Typical (days) |
High (days) |
|
Circuit breakers |
0.5 |
1.5 |
3 |
2792 |
4167 |
58333 |
|
Compressors centrifugal |
0.5 |
1.9 |
3 |
833 |
2500 |
5000 |
|
Compressor blades |
0.5 |
2.5 |
3 |
16667 |
33333 |
62500 |
|
Compressor vanes |
0.5 |
3 |
4 |
20833 |
41667 |
83333 |
|
Diaphgram couplings |
0.5 |
2 |
4 |
5208 |
12500 |
25000 |
|
Gas turb. comp. blades/vanes |
1.2 |
2.5 |
6.6 |
417 |
10417 |
12500 |
|
Gas turb. blades/vanes |
0.9 |
1.6 |
2.7 |
417 |
5208 |
6667 |
|
Motors AC |
0.5 |
1.2 |
3 |
42 |
4167 |
8333 |
|
Motors DC |
0.5 |
1.2 |
3 |
4 |
2083 |
4167 |
|
Pumps centrifugal |
0.5 |
1.2 |
3 |
42 |
1458 |
5208 |
|
Steam turbines |
0.5 |
1.7 |
3 |
458 |
2708 |
7083 |
|
Steam turbine blades |
0.5 |
2.5 |
3 |
16667 |
33333 |
62500 |
|
Steam turbine vanes |
0.5 |
3 |
3 |
20833 |
37500 |
75000 |
|
Transformers |
0.5 |
1.1 |
3 |
583 |
8333 |
591667 |
|
Instrumentation |
Low |
Typical |
High |
Low (days) |
Typical (days) |
High (days) |
|
Controllers pneumatic |
0.5 |
1.1 |
2 |
42 |
1042 |
41667 |
|
Controllers solid state |
0.5 |
0.7 |
1.1 |
833 |
4167 |
8333 |
|
Control valves |
0.5 |
1 |
2 |
583 |
4167 |
13875 |
|
Motorized valves |
0.5 |
1.1 |
3 |
708 |
1042 |
41667 |
|
Solenoid valves |
0.5 |
1.1 |
3 |
2083 |
3125 |
41667 |
|
Transducers |
0.5 |
1 |
3 |
458 |
833 |
3750 |
|
Transmitters |
0.5 |
1 |
2 |
4167 |
6250 |
45833 |
|
Temperature indicators |
0.5 |
1 |
2 |
5833 |
6250 |
137500 |
|
Pressure indicators |
0.5 |
1.2 |
3 |
4583 |
5208 |
137500 |
|
Flow instrumentation |
0.5 |
1 |
3 |
4167 |
5208 |
416667 |
|
Level instrumentation |
0.5 |
1 |
3 |
583 |
1042 |
20833 |
|
Electro-mechanical parts |
0.5 |
1 |
3 |
542 |
1042 |
41667 |
|
Static Equipment |
Low |
Typical |
High |
Low (days) |
Typical (days) |
High (days) |
|
Boilers condensers |
0.5 |
1.2 |
3 |
458 |
2083 |
137500 |
|
Pressure vessels |
0.5 |
1.5 |
6 |
52083 |
83333 |
1375000 |
|
Filters strainers |
0.5 |
1 |
3 |
208333 |
208333 |
8333333 |
|
Check valves |
0.5 |
1 |
3 |
4167 |
4167 |
52083 |
|
Relief valves |
0.5 |
1 |
3 |
4167 |
4167 |
41667 |
|
Service Liquids |
Low |
Typical |
High |
Low (days) |
Typical (days) |
High (days) |
|
Coolants |
0.5 |
1.1 |
2 |
458 |
625 |
1375 |
|
Lubricants screw compr. |
0.5 |
1.1 |
3 |
458 |
625 |
1667 |
|
Lube oils mineral |
0.5 |
1.1 |
3 |
125 |
417 |
1042 |
|
Lube oils synthetic |
0.5 |
1.1 |
3 |
1375 |
2083 |
10417 |
|
Greases |
0.5 |
1.1 |
3 |
292 |
417 |
1375 |
Weibull Results Interpretation
GE Digital APM Reliability shows the failure pattern of a single piece of equipment or groups of similar equipment using Weibull analysis methods. This helps you determine the appropriate repair strategy to improve reliability.
Is the Probability Plot a good fit?
Follow these steps to determine whether or not the plot is a good fit:
- Identify Beta (slope) and its associated failure pattern.
- Compare Eta (characteristic life) to standard values.
- Check goodness of fit, compare with Weibull database.
- Make a decision about the nature of the failure and its prevention.
The following chart demonstrates how to interpret the Weibull analysis data using the Beta parameter, Eta parameter, and typical failure mode to determine a failure cause.
| Weibull Results | Interpretation | ||
|---|---|---|---|
|
Beta |
Eta |
Typical Failure Mode |
Failure Cause |
|
Greater than 4 |
Low compared with standard values for failed parts (less than 20%) |
Old age, rapid wear out (systematic, regular) |
Poor machine design |
|
Greater than 4 |
Low compared with standard values for failed parts (less than 20%) |
Old age, rapid wear out (systematic, regular) |
Poor material selection |
|
Between 1 and 4 |
Low compared with standard values for failed parts (less than 20%) |
Early wear out |
Poor system design |
|
Between 1 and 4 |
Low |
Early wear out |
Construction problem |
|
Less than 1 |
Low |
Infant Mortality |
Inadequate maintenance procedure |
|
Between 1 and 4 |
Between 1 and 4 |
Less than manufacturer recommended PM cycle |
Inadequate PM schedule
|
|
Around 1 |
Much less than |
Random failures with definable causes |
Inadequate operating procedure |
Goodness of Fit (GOF) Tests for a Weibull Distribution
A Goodness of Fit test is a statistical test that determines whether the analysis data follows the distribution model.
- If the data passes the Goodness of Fit test, it means that it follows the model pattern closely enough that predictions can be made based on that model.
- If the data fails the Goodness of Fit test, it means that the data does not follow the model closely enough to confidently make predictions and that the data does not appear to follow a specific pattern.
Weibull results are valid if Goodness of Fit (GOF) tests are satisfied. Goodness of Fit tests for a Weibull distribution include the following types:
- R-Squared Linear regression (least squares): An R-Squared test statistic greater than 0.9 is considered a good fit for linear regression.
- Kolmogorov-Smirnov: The GE Digital APM system uses confidence level and P-Value to determine if the data is considered a good fit. If the P-Value is greater than 1 minus the confidence level, the test passes.
About Exponential Distribution
An Exponential Distribution is a mathematical distribution that describes a purely random process. It is a single parameter distribution where the mean value describes MTBF (Mean Time Between Failures). It is simulated by the Weibull distribution for value of Beta = 1. When applied to failure data, the Exponential distribution exhibits a constant failure rate, independent of time in service. The Exponential Distribution is often used in reliability modeling, when the failure rate is known but the failure pattern is not.
An Exponential Distribution uses the following parameter:
- MTBF: Mean time between failures calculated for the analysis.
About Lognormal Distribution
In Lognormal Distributions of failure data, two parameters are calculated: Mu and Sigma. These do not represent mean and standard deviation, but they are used to calculate MTBF. In Lognormal analysis, the median (antilog of mu) is often used as the MTBF. The standard deviation factor (antilog of sigma) gives the degree of variance in the data.
A Lognormal Distribution uses the following parameters:
- Mu: The logarithmic average for the Distribution function.
- Sigma: The scatter.
- Gamma: A location parameter.
About Triangular Distribution
Triangular Distribution is typically used as a subjective description of a population for which there is only limited sample data, and especially in cases where the relationship between variables is known, but data is scarce (possibly because of the high cost of collection). It is based on a knowledge of the minimum (a) and maximum (b) and an inspired guess as to the modal value (c).
- Lower limit a
- Upper limit b
- Mode c
…where a < b and a ≤ c ≤ b.
About Gumbel Distribution
The Gumbel Distribution is a continuous probability distribution. Gumbel distributions are a family of distributions of the same general form. These distributions differ in their location and scale parameters: the mean of the distribution defines its location, and the standard deviation, or variability, defines the scale.
The Gumbel Distribution is a probability distribution of extreme values.
In probability theory and statistics, the Gumbel distribution is used to model the distribution of the maximum (or the minimum) of a number of samples of various distributions.
About Generalized Extreme Value Distribution
In probability theory and statistics, the Generalized Extreme Value (GEV) Distribution is a family of continuous probability distributions developed within extreme value theory.
By the Extreme Value Theorem, the GEV Distribution is the only possible limit distribution of properly normalized maxima of a sequence of independent and identically distributed random variables.
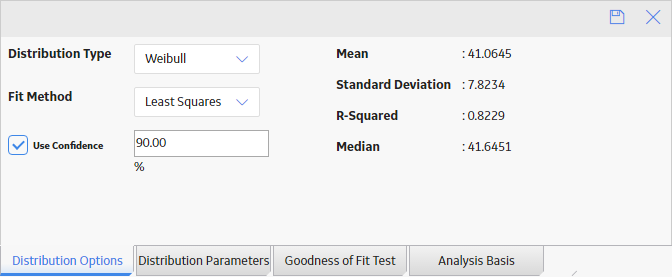
Change the Distribution Parameters in a Probability Distribution Analysis
About this task
This topic describes how to modify the values of the distribution parameters in a Probability Distribution Analysis.
You can change the distribution parameters from the Analysis Summary workspace or from any of the plot tabs in the left pane.
Procedure
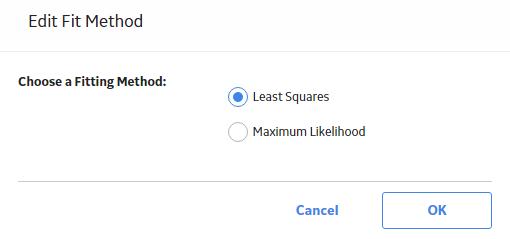
Change the Fit Method of a Probability Distribution Analysis
About this task
The Kolmogorov-Smirnov test is a Goodness of Fit (GOF) test applied to a Probability Distribution Analysis to determine how well the data fits the analytical curve. When you create an analysis, the fit method is set to Least Squares by default.
After the analysis is created, you can modify the fit method to one of the following:
- Least Squares: A curve-fitting estimation method that relies on linear regression techniques to estimate the parameters for the distribution.
- Maximum Likelihood Estimators: A curve-fitting estimation method that maximizes the likelihood function for a given population. This method includes a survivor function that estimates changes in reliability as the piece of equipment or location survives beyond a certain age.
You can change the fit method from the Analysis Summary workspace or from any of the plot tabs in the left pane.
Procedure
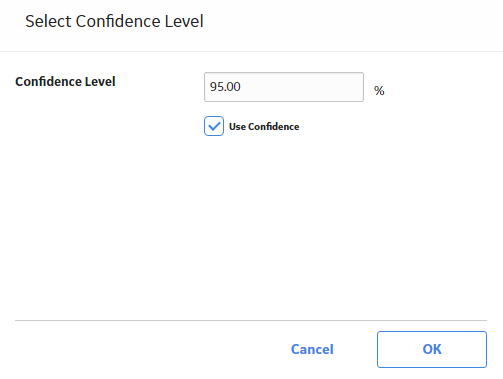
Modify the Confidence Level for a Probability Distribution Analysis
About this task
The Confidence Level specifies how the optimistic and realistic scenarios will be selected in a Monte Carlo Simulation for TTR Distributions in an analysis. The Confidence Level indicates whether the distribution is within the confidence limits or not. The default Confidence Level for an analysis is 90 percent.
You can modify the Confidence Level from the Analysis Summary workspace or from any of the plot tabs in the left pane.
Procedure
Modify the Random Variable and Specify Units for a Probability Distribution Analysis
Procedure
Rename a Probability Distribution Analysis
Procedure
Access the Source Data for a Probability Distribution Analysis
Procedure
Modify Data in a Probability Distribution Analysis
Procedure
Results
- For an analysis that is based on manually entered data, the changes that you make via the Probability Distribution Data window will be saved for the analysis.
- For an analysis that is based on a query or a dataset:
- The query or dataset will not be modified with the updated data. Additionally, any record returned by the query will not be updated with your changes. The changes will be saved to the analysis only.
- After you modify the data and save the analysis, the modified data will appear each time you open the analysis. If you want to revert to the original data, you can reload the original data to the analysis. In addition, if a query or dataset has changed in the database, you can reload the data in order for your analysis to contain those changes.
Reload Analysis Data in a Probability Distribution Analysis
About this task
When you create and save an analysis that is based on a query or dataset, the GE Digital APM system takes a snapshot of the data that exists at the time of creation and saves it along with the analysis. When you open an existing analysis, the GE Digital APM system loads the data that was last saved with the analysis. This means that any changes to the underlying query or dataset will not be reflected automatically when you open an existing analysis.
If you want to refresh an analysis based upon changes to the underlying query or dataset or to load new data that has been added since the analysis was last saved (e.g., the analysis is based on a query that retrieves failures for a piece of equipment or location, and a new failure record has been added to the database), you will need to reload the analysis manually after opening it. When you reload the data, any manual changes made to the analysis data set will be deleted.
Procedure
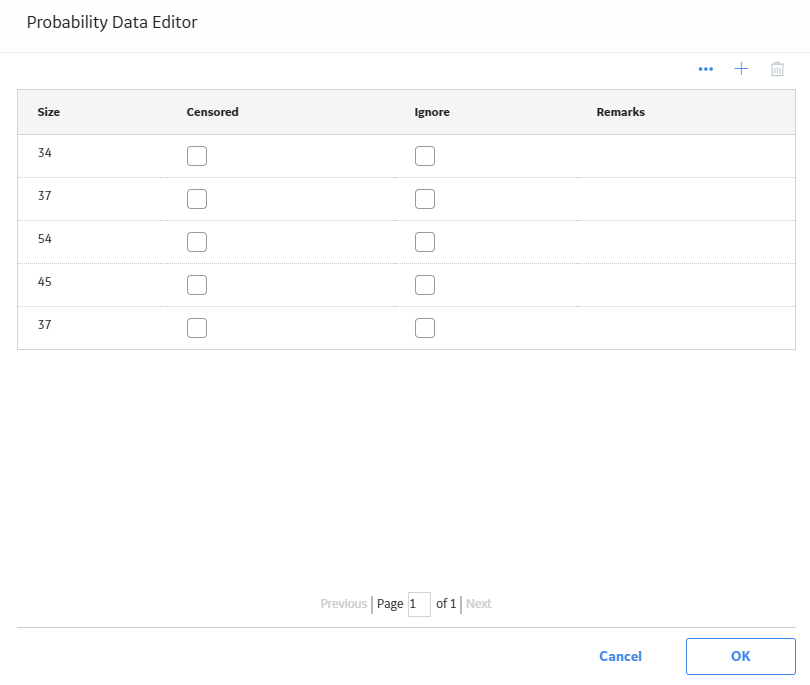
Censor Data in a Probability Distribution Analysis
Procedure
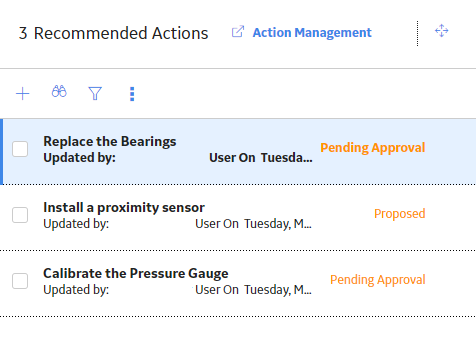
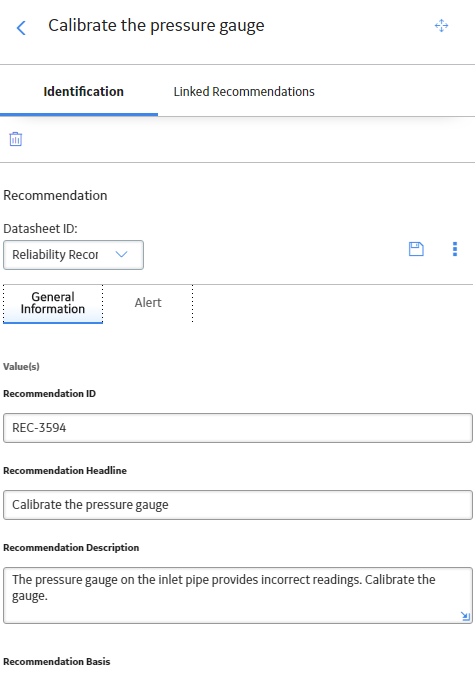
Access a Recommendation
Procedure
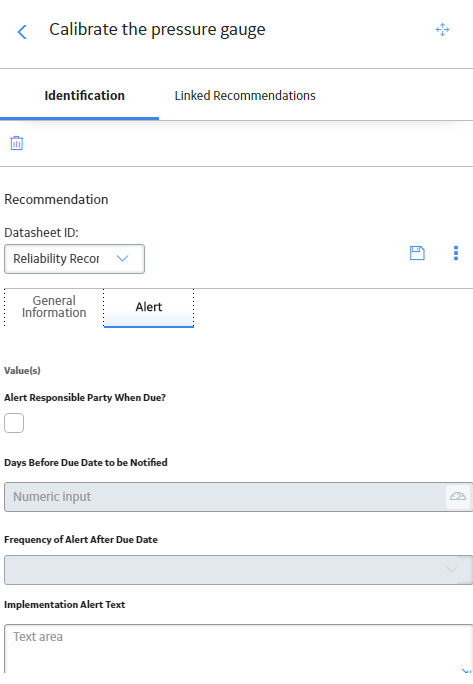
Create a Recommendation Alert for an Analysis
Procedure
Delete a Probability Distribution Analysis
Procedure
Access Probability Distribution Report
Procedure
About Probability Distribution Report
The baseline GE Digital APM database includes the Probability Distribution report, which you can use to view a summary of the results of a Probability Distribution Analysis.
The Probability Distribution report is built from the following Catalog items:
- The subreport, SubReportProbDist, which is stored in the Catalog folder \\Public\Meridium\Modules\Reliability Manager\Reports.
- The supporting queries that supply data in the main report and subreport, which are stored in the Catalog folder \\Public\Meridium\Modules\Reliability Manager\Reports. The following supporting queries are available:
- ProbabilityDistributionQuery
- Weibull Distribution Query
- Lognormal Distribution Query
- Normal Distribution Query
- Exponential Distribution Query
Throughout this documentation, we refer to the main report, the subreport, and the supporting queries collectively as the Probability Distribution report.
The Probability Distribution report contains a prompt on the ENTY KEY and Distribution Type fields in the Distribution family. When you run the Probability Distribution report via the Probability Distribution module, the ENTY KEY and Distribution Type of the Distribution record associated with the current analysis is passed automatically to the prompt, and the results for the current Probability Distribution Analysis are displayed. If you run the main report or any of the queries in the preceding list directly from the Catalog, however, you will need to supply the ENTY KEY and Distribution Type of a Distribution record manually to retrieve results. The subreport (i.e., Catalog item SubReportProbDist) cannot be run directly from the Catalog.
Analysis Summary Section
The Analysis Summary section of the Probability Distribution report displays information that is stored in a Distribution record. Distribution records are categorized into one of four Distribution subfamilies: Exponential, Lognormal, Normal, or Weibull.
The following table lists each item in the Analysis Summary section and the corresponding Distribution record field whose data is displayed in the report.
| Report Item | Distribution record |
|---|---|
| Analysis Name | Analysis ID |
| Analysis Description | Short Description |
| Random Variable | Random Variable Field |
| Units | Units |
| Last Modified | LAST UPDT DT |
| Modified By |
LAST UPBY SEUS KEY Note: The name of the Security User associated with this value is displayed in the report.
|
Statistical Distribution Information Section
The Statistical Distribution Information section of the Probability Distribution report displays information that is stored in the Distribution record (i.e., Exponential, Lognormal, Normal, or Weibull record).
The following subsections are displayed within the Statistical Distribution Information section:
The Distribution Type subsection displays information that is stored in the Distribution record. Throughout the documentation, we will refer to this subsection as the Distribution subsection.
The following table lists each item in the Distribution subsection and the corresponding Distribution record field whose data is displayed in the report.
| Report Item | Distribution Field |
|---|---|
| Distribution Type |
Distribution Type |
| Fit Method |
Fit Method |
| Use Confidence |
Use Confidence |
| Confidence Level | Confidence Level |
| Mean | Mean |
| Standard Deviation | Standard Deviation |
| Median |
Median |
| R2 | R-Squared |
The Parameters subsection contains information stored in the Distribution record. The type of information that appears in the Parameters subsection depends on the distribution type (i.e., Weibull, Lognormal, Exponential, or Normal).
The following table lists each item in the Parameters subsection for a Weibull record whose data is displayed in the report. One row is displayed for each of the following field captions: Beta, Eta, and Gamma.
| Report Item | Weibull Field |
|---|---|
| Beta | |
| Value |
Beta |
| Low |
Beta Low |
| High | Beta High |
| Calculated | Beta Fixed |
| Eta | |
| Value | Eta |
| Low | Eta Low |
| High |
Eta High |
| Calculated | Eta Fixed |
| Gamma | |
| Value | Gamma |
| Low | Gamma Low |
| High |
Gamma High |
| Calculated | Gamma Fixed |
The following table lists each item in the Parameters subsection for a Lognormal record whose data is displayed in the report. For a Lognormal record, one row is displayed for each of the following field captions: Mu, Sigma, and Gamma.
| Report Item | Lognormal Field |
|---|---|
| Mu | |
| Value |
Mu |
| Low |
Mu Low |
| High | Mu High |
| Calculated | Mu Fixed |
| Sigma | |
| Value | Sigma |
| Low | Sigma Low |
| High |
Sigma High |
| Calculated | Sigma Fixed |
| Gamma | |
| Value | Gamma |
| Low | Gamma Low |
| High |
Gamma High |
| Calculated | Gamma Fixed |
The following table lists each item in the Parameters subsection for an Exponential record whose data is displayed in the report. For an Exponential record, one row is displayed for the field caption MTBF.
| Report Item | Exponential Field |
|---|---|
| MTBF | |
| Value |
MTBF |
| Low |
MTBF Low |
| High | MTBF High |
| Calculated | MTBF Fixed |
The following table lists each item in the Parameters subsection for a Normal record whose data is displayed in the report. For a Normal record, one row is displayed for each of the following field captions: Mean, Standard Deviation.
| Report Item | Normal Field |
|---|---|
| Mean | |
| Value |
Mean |
| Low |
Mean Low |
| High | Mean High |
| Calculated | Mean Fixed |
| Standard Deviation | |
| Value | Standard Deviation |
| Low | Standard Deviation Low |
| High |
Standard Deviation High |
| Calculated | Standard Deviation Fixed |
The Goodness of Fit Test subsection displays information from the Distribution record.
The Kolmogorov-Smirnov test is the only test used to measure goodness of fit, so the Name column in the report is populated with the value Kolmogorov-Smirnov Test.
The following table lists each remaining item in the Goodness of Fit Test subsection and the Distribution record field whose data is displayed in the report.
| Report Item | Weibull Field |
|---|---|
| Statistic |
GOF Statistic |
| P-Value |
GOF P-Value |
| Passed |
Passed |
Distribution Data Section
The Distribution Data section of the Probability Distribution report displays information that is stored in the Data field in the Distribution record.
The following values are displayed in the Distribution Data section, and they are stored in the Data field in the Reliability Distribution record:
- X (i.e., the Random Variable)
- Censored
- Ignored
- Remarks
Plots Section
The Plots section of the Probability Distribution report displays the plots that are displayed on the Analysis Summary workspace or accessed via the Plots tabs in the left pane on the Probability Distribution page.
The Plots section displays the following graphs:
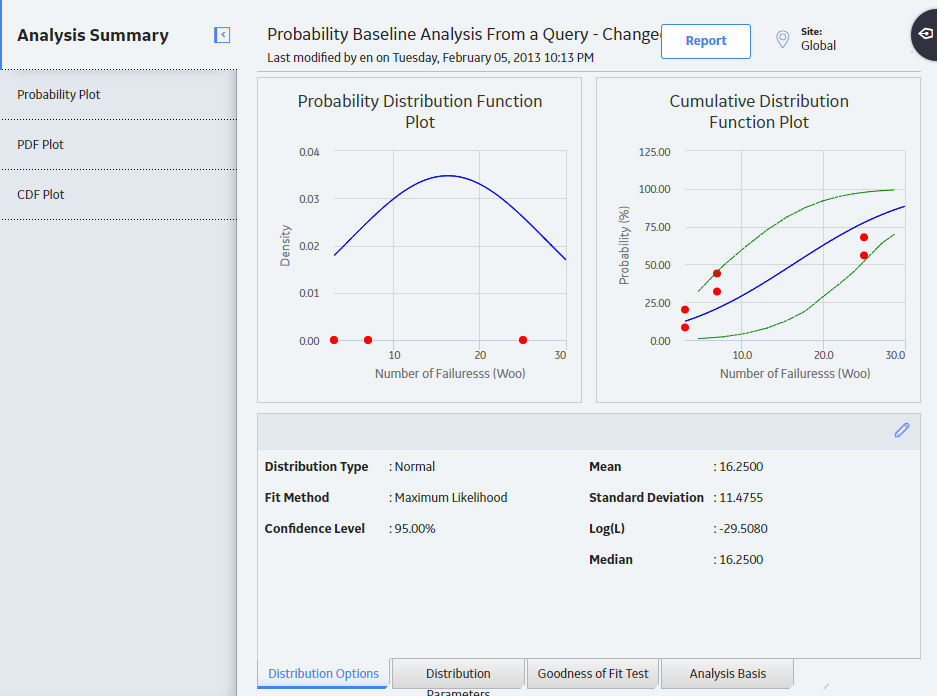
 .
.




 .
.
 .
.
 , and the previous selection will be used in the calculations.
, and the previous selection will be used in the calculations.
 .
.
 .
.