Simulations
About Monte Carlo Simulations
APM System Reliability Analysis uses Monte Carlo simulations to predict the reliability of a system. Monte Carlo methods offer a common statistical model for simulating physical systems and are especially useful for modeling systems with variable and uncertain inputs. When you create a System Reliability Analysis, you will specify certain values that will serve as inputs to the simulation. Other inputs will be generated at random to simulate possible conditions. Outputs will be generated based on the inputs and combined to provide a summary the projected system reliability.
Details
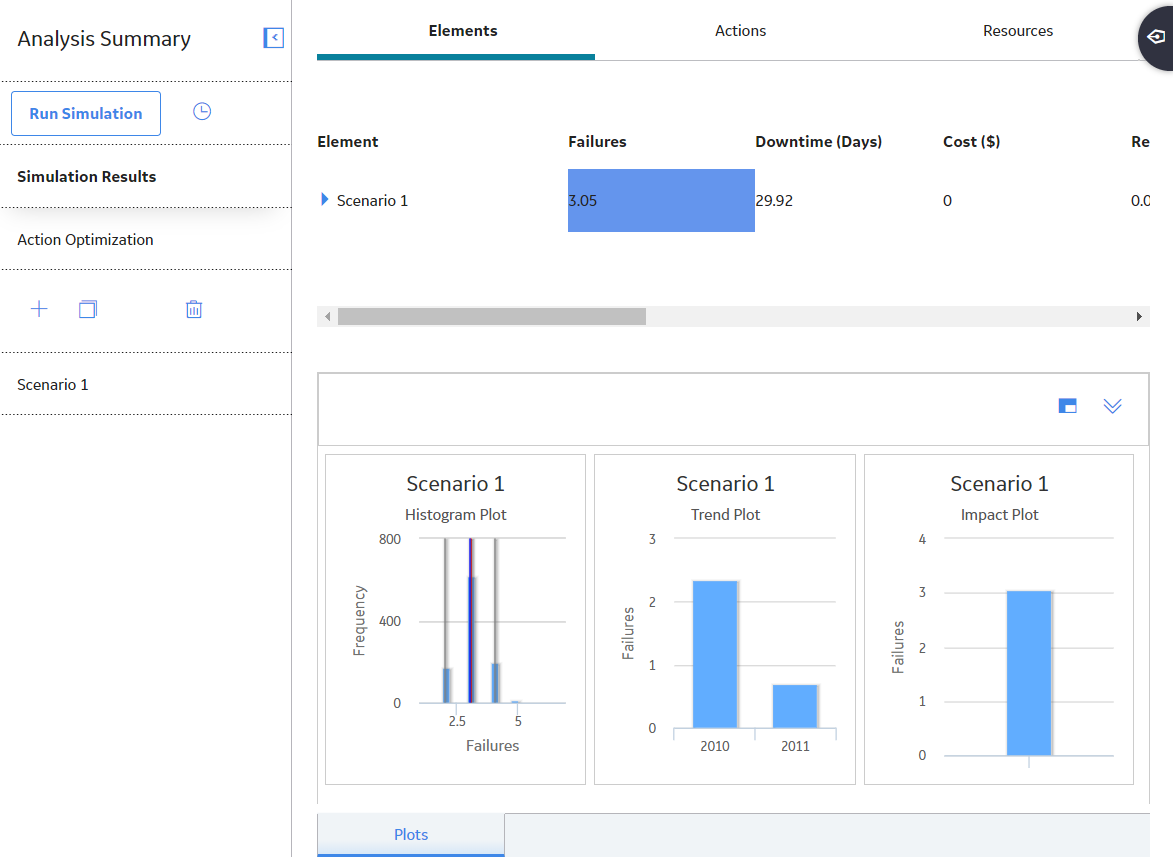
When you run a simulation, you start the process of running Monte Carlo iterations for each Scenario in a System Reliability Analysis and accessing the results calculated from those simulations. When you run the simulation, all Diagrams are validated.
You need to run a simulation, if you make changes to a System Reliability Analysis that would affect the simulation results, such as changing the simulation parameters or modifying a Scenario.
It takes time to run simulations. Various factors influence the speed of the simulation process, including:
- The number of iterations defined.
- The complexity of the Scenarios (i.e., the number of Assets, Risks, Actions, and Subsystems).
- The frequency at which Actions occur.
- The frequency at which failures occur.
To shorten the run time of your simulation, you can reduce the number of iterations or the complexity of the analysis.
You can run only one simulation at a time for an analysis. For example, if you are running a simulation for Analysis A, you cannot run another simulation for Analysis A. You can, however, run simulation for Analysis B while running the simulation for Analysis A. While a simulation is running, you can continue working in other areas of APM.
Rolling a Dice
Consider a simple example of rolling dice. Assume that you want to determine the probability of rolling a seven using two dice with values one through six. There are 36 possible combinations for the two dice, six of which will total seven, as shown in the following image.

This means that mathematical probability of rolling a seven is six in 36, or 16.67 percent.
But is the mathematical probability the same as the actual probability? Or are there other factors that might affect the mathematical probability, such as the design of the dice themselves, the surface on which they are thrown, and the technique that is used to roll them?
To determine the actual probability of rolling a seven, you might physically roll the dice 100 times and record the outcome each time. Assume that you did this and rolled a seven 17 out of 100 times, or 17 percent of the time. Although this result would represent an actual, physical result, it would still represent an approximate result. If you continued to roll the dice again and again, the result would become less and less approximate.
A Monte Carlo simulation is the mathematical representation of this process. It allows you to simulate the act of physically rolling the dice and lets you specify how many times to roll them. Each roll of the dice represents a single iteration in the overall simulation; as you increase the number of iterations, the simulation results become more and more accurate. For each iteration, variable inputs are generated at random to simulate conditions such as dice design, rolling surface, and throwing technique. The results of the simulation would provide a statistical representation of the physical experiment described above.