Rates and Calculations
Interest Rate Definitions
There are several types of interest rates used in LCC Analyses.
The differences among the various types of rates are based on several key economic factors.
Annual Nominal Interest Rates
The annual nominal interest rate is the stated interest rate of a given loan. It is the actual monetary price that borrowers pay to lenders to use their money. If the nominal rate on a loan is 5%, then borrowers can expect to pay $5 of interest for every $100 loaned to them for one year.
Simple Interest Rates
Simple interest rate is the easiest to calculate as there is no compounding taking place over each year. So, a 5% simple annual interest rate adds 5 percent to the capital sum owed for each year.
Simple Interest Rates
If you put a sum of money in the bank and spend the interest earned each year (i.e., the capital stays constant), the amount of money that you will have earned some time in the future is given by the formula:
A=P(1+r)*t
where P is the initial investment (Principal), r is the interest rate per period expressed as a decimal fraction, t is the number of periods, and A is the amount of money in the bank plus the interest you spend at the end of the calculated period.
Compounded Interest Rates
In compounded interest rates, the rate of annual interest is applied to the principle sum borrowed, plus the additional amount owed in the previous year due to the interest already applied.
Compounded Interest Rates
If you put a sum of money in the bank and let the interest accumulate, the amount of money that you will have some time in the future is given by the formula:
A=P(1+r)^t
where P is the initial investment, r is the interest rate per period, t is the number of periods, and A is the amount of money in the bank after the periods.
Real Interest Rates
The real interest rate states the “real” rate that the lender receives after inflation is factored in; that is, the interest rate that exceeds the inflation rate. If a bond that compounds annually has a 6% nominal yield and the inflation rate is 4%, then the real rate of interest is only 2%.
The real rate of interest could be said to be the actual mathematical rate at which investors and lenders are profiting from their loans. It is actually possible for real interest rates to be negative if the inflation rate exceeds the nominal rate of an investment. For example, a bond with a 3% nominal rate will have a real interest rate of -1% if the inflation rate is 4%. A comparison of real and nominal interest rates can therefore be summed up in this equation:
Real interest rate = Nominal interest rate – Inflation
Several economic stipulations can be derived from this formula that lenders, borrowers and investors can use to make more informed financial decisions.
Real interest rates can not only be positive or negative, but can also be higher or lower than nominal rates. Nominal interest rates will exceed real rates when the inflation rate is a positive number (as it usually is). But, real rates can also exceed nominal rates during deflation periods.
Annual Effective Interest Rates
The effective rate takes the power of compounding into account for Nominal Interest Rate. For example, if a bond pays 6% on an annual basis and compounds semiannually, then an investor who invests $1,000 in this bond will receive $30 of interest after the first 6 months ($1,000 x .03), and $30.90 of interest after the next 6 months ($1,030 x .03). The investor received a total of $60.90 for the year, which means that while the nominal rate was 6%, the effective rate was 6.09%.
Mathematically speaking, the difference between the nominal and effective rates increases with the number of compounding periods within a specific time period.
Depreciation Methods
Depreciation Methods include:
Declining Balance
Declining balance method of depreciation is a technique of accelerated depreciation in which the amount of depreciation that is charged to an asset declines over time. In other words, more depreciation is charged during the beginning of the lifetime and less is charged during the end.
The reason for a declining amount of depreciation charged is that assets are usually more productive when they are new and their productivity declines gradually. Thus, in the early years of their operation, assets generate more revenue as compared to the revenue generated in later years of their life.
Formula and Calculation Procedure
Declining balance depreciation is calculated using the following formula:
Depreciation = Depreciation Rate × Book Value of Asset
Depreciation rate is given by the following formula:
Depreciation Rate = Accelerator × Straight Line Rate
In the above formula, accelerator is a multiplication factor, which accelerates depreciation. Book value is the difference between cost of an asset and its accumulated depreciation. During the first accounting period, accumulated depreciation is zero, so book value is equal to cost. Since the book value decreases after each depreciation charge, depreciation expense declines in successive charges.
Depreciation is charged according to the above method as long as book value is greater than the salvage value of the asset. No more depreciation is provided when book value equals salvage value.
Single Line
Single line (or Straight line) depreciation is the default method used to gradually reduce the carrying amount of a fixed asset over its useful life. The method is designed to reflect the consumption pattern of the underlying asset, and is used when there is no particular pattern to the manner in which the asset is to be used over time.
- Under the straight-line method of depreciation, depreciation occurs evenly over the estimated useful life of an asset. The straight-line calculation steps are:
- Determine the initial cost of the asset that has been recognized as a fixed asset.
- Subtract the estimated salvage value of the asset from the amount at which it is recorded on the books.
- Determine the estimated useful life of the asset. It is easiest to use a standard useful life for each class of assets.
- Divide the estimated useful life (in years) into 1 to arrive at the straight-line depreciation rate.
- Multiply the depreciation rate by the asset cost (less salvage value).
Single Line
Pensive Corporation purchases the Procrastinator Deluxe machine for $60,000. It has an estimated salvage value of $10,000 and a useful life of five years. Pensive calculates the annual straight-line depreciation for the machine as:
- Purchase cost of $60,000 – estimated salvage value of $10,000 = Depreciable asset cost of $50,000
- 1 / 5-year useful life = 20% depreciation rate per year
- 20% depreciation rate x $50,000 depreciable asset cost = $10,000 annual depreciation
Sum of Years
The sum-of-years digits depreciation method is an accelerated method of depreciation that calculates depreciation using the following equation:
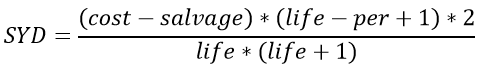
where,
cost = initial cost of the asset (at start of period 1)
salvage = final value of the asset at the end of its lifetime
life = number of periods over which the depreciation occurs
per = the period for which the depreciation is being calculated
Straight Line
Straight line is the sum of capital costs and number of periods.
Annual (Straight Line) Depreciation Rate DSL = (V-S)/(V*L)
Annual Discount Rate
The annual discount rate is the rate of return used in a discounted cash flow analysis to determine the present value of future cash flows.
Details
In an annual discounted cash flow analysis, the sum of all future cash flows (C) over some holding period (N), is discounted back to the present using a rate of return (r). This rate of return (r) in the below formula is the discount rate.
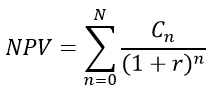
Net Present Value
The net present value (NPV) or net present worth (NPW)[1] is defined as the sum of the present values (PVs) of incoming and outgoing cash flows over a period of time. Incoming and outgoing cash flows can also be described as benefit and cost cash flows, respectively.
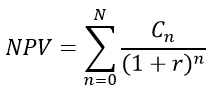
Present Value
Present value is the current value of future cash flows base on the Discount Rate. For LCC, the Discount Rate is calculated from Nominal Interest Rate to give the time value of money being applied.
(Cash Flow / (1+Discount Rate))
Costs
Costs include:
Capital Costs
Capital costs are costs, typically recurring, which are set in advance and do not vary. Examples include storage overheads amortized over the total number of assets, documentation, etc.
Cash Flow
Cash flow represents the after tax influx of money, which can be positive if savings are considered.
(Revenue - (All Costs + Depreciation)) * (1-Tax Rate) + Depreciation
Operational Costs
Operational costs are the sum of operation costs for a period and includes all variable costs related to operating the equipment (e.g., fuel and maintenance).
Revenue
Revenue is calculated from the Profile.
Total Cost of Ownership
Total Cost of Ownership represents the sum of all cash flows after tax cost over the life cycle of the asset.
Annual Escalation Rate
Annual Escalation Rate = current cost or value minus the initial price or value and divide by the initial price in a one year period.
ER = (C2 – C1) / C1, where C1 is initial cost and C2 is the end value after 1 year
Internal Rate of Return
Internal Rate of Return represents the interest rate required to bring the Net Present Value (NPV) to zero, and gives the anticipated return rate from investment in the asset (Total Cost of Ownership).
TCO / (1 + Discount Rate)
Planned Unit Consumption
Planned Unit Consumption is the sum of all operating units accumulated over each period in an analysis.
Equivalent Unit Cost
Equivalent Unit Cost is the present value of the average cost per operating unit.